Batch Normalization

The main motivation for purposing Batch Normalization was to ease the training of deep learning models and help it converge faster. Deep Neural Networks are composed of multiple layers stacked on top of each others. During the forward propagating the input data is passed through all the layers and on doing so there is change in distribution of the inputs to each layer which is called as Internal Covariate shift. Lets visualize this mathematically with simple example:

Relation with activation function

Before going onto the Batch Normalization, lets see some properties of some activation function.

Tanh

Here I will not be listing formula and graph of Tanh, as I guess most of us are familiar.

g = torch.Generator().manual_seed(2147483647)
x = torch.randn((500, 16), requires_grad=True, generator=g)
weights = torch.randn((500, 500), requires_grad=True, generator=g)

net = weights @ x 

non_linearity = torch.tanh(net)


plt.hist(non_linearity.view(-1).tolist(), 50);

This is a simple prototype of neural network with Tanh activation, and plot of the results after applying Tanh is depicted below:

So we can see from the above histogram that Tanh takes most of the value to -1 and 1. And this is because of the reason that the input to the Tanh has a broad distribution and Tanh squash the exterme values to -1 and 1. Lets see the distribution of input to the Tanh:

plt.hist(net.view(-1).tolist(), 50);

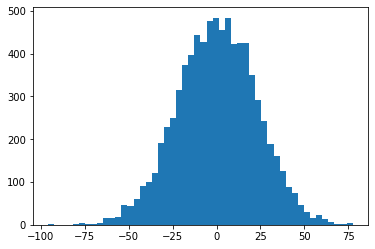
Now during back-propagation this nature of activation function will cause the problem. Lets see the gradient function of Tanh function used during back-propagation:

grad_for_tan_h = += (1 - tanh**2) * previous_layer_grad

I wrote here previous_layer_grad because it’s not important to show what I actually want. Here,

if:
tanh = -1 or 1 
than grad_for_tan_h = 0

Now when we provide more and more samples to the network in the hope of getting our weights and bias better and better during training, but this doesn’t happen because of the gradient of tanh being zero will destroy all the gardient of the network and make them inactivate.

Similar is the case with other activation function like Sigmoid and ReLU but this is not the case with Leaky ReLU, Maxout and ELU.

Batch Normalization:

We saw the problem with the non-linearity and also got the idea that we have to be careful with the weight initialization as well. Now, if we expand this simple idea to bigger neural network then things get complicated and these problems get stacked and lets see how we can solve this problem using Batch Normalization.

x = torch.randn(500, 10)
w = torch.rand(10, 200)

y = x @ w

print(x.mean(), x.std())
print(y.mean(), y.std())

plt.figure(figsize=(10,5))
plt.subplot(121)
plt.hist(x.view(-1).tolist(), 50, density=True);
plt.subplot(122)
plt.hist(y.view(-1).tolist(), 50, density=True);

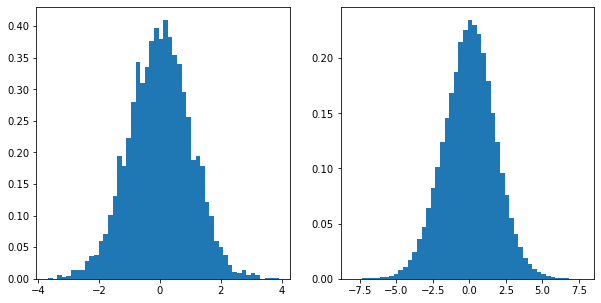
We can see here the mean is similar to the input but the variance or standard deviation has increased which when passed to non-linearity function causes the problem. So, Batch Normalization helps to keep the distribution of these value similar by nomalizing these values by standard deviation which in turn helps training and convergence of neural network.